Después de hacer una ingeniería pensaba que lo que me quedaba por saber de matemáticas eran temas avanzados o relativamente raros, pero esta semana he descubierto una relación que no recuerdo haber sabido nunca. La suma de los números impares es un cuadrado perfecto. Es decir:
1 + 3 = 4 = 2 x 2
1 + 3 + 5 = 9 = 3 x 3
1 + 3 + 5 + 7 = 16 = 4 x 4
Y así sucesivamente.
La demostración gráfica es preciosa:
El punto negro es 1. Para hacer un cuadrado hay que añadir tres puntos rojos. Para crear un cuadrado más grande hay que añadir 5 puntos verdes. Y para ir ampliando el cuadrado siempre hay que ir añadiendo el mismo número de puntos que antes más dos. Y el número de puntos totales es un cuadrado perfecto. Luego la suma de los impares es siempre un cuadrado perfecto.
La demostración algebraica es algo más complicada, pero también bonita. Primero hay que lograr la fórmula de una suma de enteros. Esto lo dedujo Gauss y la fórmula es muy estética. Llamemos S a la suma de n número de enteros consecutivos:
S = 1 + 2 + 3 + ... + (n-2) + (n-1) + n
Si lo ordenamos en el sentido contrario:
S = n + (n-1) + (n-2) + ... + 3 + 2 + 1
Si sumamos ambas expresiones término a término:
2S = (n+ 1) + (n+1) + (n+1) + ... + (n+ 1) + (n+1) + (n+1)
Y en definitiva:
2S = n(n+1)
Y:
S = n(n+1)/2
Ahora bien, la suma que buscamos no es de todos los enteros, sino de los impares Generalicemos la expresión anterior:
Y, ¿a cuánto es igual esta expresión? Fácil:

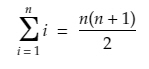


No hay comentarios:
Publicar un comentario